Теорема о приращении кинетической энергии. Московский государственный университет печати

⁰

Энергией называется скалярная физическая величина, являющаяся единой мерой различных форм движения материи и мерой перехода движения материи из одних форм в другие.

Для характеристики различных форм движения материи вводятся соответствующие виды энергии, например: механическая, внутренняя, энергия электростатических, внутриядерных взаимодействий и др.

Энергия подчиняется закону сохранения, который является одним из важнейших законов природы.

Механическая энергия Е характеризует движение и взаимодействие тел и является функцией скоростей и взаимного расположения тел. Она равна сумме кинетической и потенциальной энергий.

Кинетическая энергия

Рассмотрим случай, когда на тело массой m действует постоянная сила \(~\vec F\) (она может быть равнодействующей нескольких сил) и векторы силы \(~\vec F\) и перемещения \(~\vec s\) направлены вдоль одной прямой в одну сторону. В этом случае работу силы можно определить как A = F ∙s . Модуль силы по второму закону Ньютона равен F = m∙a , а модуль перемещения s при равноускоренном прямолинейном движении связан с модулями начальной υ 1 и конечной υ 2 скорости и ускорения а выражением \(~s = \frac{\upsilon^2_2 - \upsilon^2_1}{2a}\) .

Отсюда для работы получаем

\(~A = F \cdot s = m \cdot a \cdot \frac{\upsilon^2_2 - \upsilon^2_1}{2a} = \frac{m \cdot \upsilon^2_2}{2} - \frac{m \cdot \upsilon^2_1}{2}\) . (1)

Физическая величина, равная половине произведения массы тела на квадрат его скорости, называется кинетической энергией тела .

Кинетическая энергия обозначается буквой E k .

\(~E_k = \frac{m \cdot \upsilon^2}{2}\) . (2)

Тогда равенство (1) можно записать в таком виде:

\(~A = E_{k2} - E_{k1}\) . (3)

Теорема о кинетической энергии

работа равнодействующей сил, приложенных к телу, равна изменению кинетической энергии тела.

Так как изменение кинетической энергии равно работе силы (3), кинетическая энергия тела выражается в тех же единицах, что и работа, т. е. в джоулях.

Если начальная скорость движения тела массой m равна нулю и тело увеличивает свою скорость до значения υ , то работа силы равна конечному значению кинетической энергии тела:

\(~A = E_{k2} - E_{k1}= \frac{m \cdot \upsilon^2}{2} - 0 = \frac{m \cdot \upsilon^2}{2}\) . (4)

Физический смысл кинетической энергии

кинетическая энергия тела, движущегося со скоростью υ, показывает, какую работу должна совершить сила, действующая на покоящееся тело, чтобы сообщить ему эту скорость.

Потенциальная энергия

Потенциальная энергия – это энергия взаимодействия тел.

Потенциальная энергия поднятого над Землей тела – это энергия взаимодействия тела и Земли гравитационными силами. Потенциальная энергия упруго деформированного тела – это энергия взаимодействия отдельных частей тела между собой силами упругости.

Потенциальными называются силы , работа которых зависит только от начального и конечного положения движущейся материальной точки или тела и не зависит от формы траектории.

При замкнутой траектории работа потенциальной силы всегда равна нулю. К потенциальным силам относятся силы тяготения, силы упругости, электростатические силы и некоторые другие.

Силы , работа которых зависит от формы траектории, называются непотенциальными . При перемещении материальной точки или тела по замкнутой траектории работа непотенциальной силы не равна нулю.

Потенциальная энергия взаимодействия тела с Землей

Найдем работу, совершаемую силой тяжести F т при перемещении тела массой m вертикально вниз с высоты h 1 над поверхностью Земли до высоты h 2 (рис. 1). Если разность h 1 – h 2 пренебрежимо мала по сравнению с расстоянием до центра Земли, то силу тяжести F т во время движения тела можно считать постоянной и равной mg .

Так как перемещение совпадает по направлению с вектором силы тяжести, работа силы тяжести равна

\(~A = F \cdot s = m \cdot g \cdot (h_1 - h_2)\) . (5)

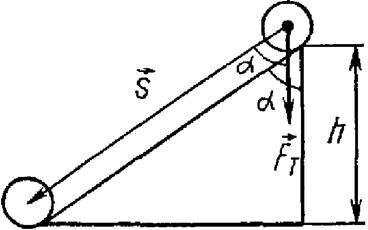
Рассмотрим теперь движение тела по наклонной плоскости. При перемещении тела вниз по наклонной плоскости (рис. 2) сила тяжести F т = m∙g совершает работу

\(~A = m \cdot g \cdot s \cdot \cos \alpha = m \cdot g \cdot h\) , (6)

где h – высота наклонной плоскости, s – модуль перемещения, равный длине наклонной плоскости.

Движение тела из точки В в точку С по любой траектории (рис. 3) можно мысленно представить состоящим из перемещений по участкам наклонных плоскостей с различными высотами h ’, h ’’ и т. д. Работа А силы тяжести на всем пути из В в С равна сумме работ на отдельных участках пути:

\(~A = m \cdot g \cdot h" + m \cdot g \cdot h"" + \ldots + m \cdot g \cdot h^n = m \cdot g \cdot (h" + h"" + \ldots + h^n) = m \cdot g \cdot (h_1 - h_2)\) , (7)

где h 1 и h 2 – высоты от поверхности Земли, на которых расположены соответственно точки В и С .

Равенство (7) показывает, что работа силы тяжести не зависит от траектории движения тела и всегда равна произведению модуля силы тяжести на разность высот в начальном и конечном положениях.

При движении вниз работа силы тяжести положительна, при движении вверх – отрицательна. Работа силы тяжести на замкнутой траектории равна нулю.

Равенство (7) можно представить в таком виде:

\(~A = - (m \cdot g \cdot h_2 - m \cdot g \cdot h_1)\) . (8)

Физическую величину, равную произведению массы тела на модуль ускорения свободного падения и на высоту, на которую поднято тело над поверхностью Земли, называют потенциальной энергией взаимодействия тела и Земли.

Работа силы тяжести при перемещении тела массой m из точки, расположенной на высоте h 2 , в точку, расположенную на высоте h 1 от поверхности Земли, по любой траектории равна изменению потенциальной энергии взаимодействия тела и Земли, взятому с противоположным знаком.

\(~A = - (E_{p2} - E_{p1})\) . (9)

Потенциальная энергия обозначается буквой Е p .

Значение потенциальной энергии тела, поднятого над Землей, зависит от выбора нулевого уровня, т. е. высоты, на которой потенциальная энергия принимается равной нулю. Обычно принимают, что потенциальная энергия тела на поверхности Земли равна нулю.

При таком выборе нулевого уровня потенциальная энергия Е p тела, находящегося на высоте h над поверхностью Земли, равна произведению массы m тела на модуль ускорения свободного падения g и расстояние h его от поверхности Земли:

\(~E_p = m \cdot g \cdot h\) . (10)

Физический смысл потенциальной энергии взаимодействия тела с Землей

потенциальная энергия тела, на которое действует сила тяжести, равна работе, совершаемой силой тяжести при перемещении тела на нулевой уровень.

В отличие от кинетической энергии поступательного движения, которая может иметь лишь положительные значения, потенциальная энергия тела может быть как положительной, так и отрицательной. Тело массой m , находящееся на высоте h , где h < h 0 (h 0 – нулевая высота), обладает отрицательной потенциальной энергией:

\(~E_p = -m \cdot g \cdot h\) .

Потенциальная энергия гравитационного взаимодействия

Потенциальная энергия гравитационного взаимодействия системы двух материальных точек с массами m и М , находящихся на расстоянии r одна от другой, равна

\(~E_p = G \cdot \frac{M \cdot m}{r}\) . (11)

где G – гравитационная постоянная, а нуль отсчета потенциальной энергии (Е p = 0) принят при r = ∞.

Потенциальная энергия гравитационного взаимодействия тела массой m с Землей, где h – высота тела над поверхностью Земли, M e – масса Земли, R e – радиус Земли, а нуль отсчета потенциальной энергии выбран при h = 0.

\(~E_e = G \cdot \frac{M_e \cdot m \cdot h}{R_e \cdot (R_e +h)}\) . (12)

При том же условии выбора нуля отсчета потенциальная энергия гравитационного взаимодействия тела массой m с Землей для малых высот h (h « R e) равна

\(~E_p = m \cdot g \cdot h\) ,

где \(~g = G \cdot \frac{M_e}{R^2_e}\) – модуль ускорения свободного падения вблизи поверхности Земли.

Потенциальная энергия упруго деформированного тела

Вычислим работу, совершаемую силой упругости при изменении деформации (удлинения) пружины от некоторого начального значения x 1 до конечного значения x 2 (рис. 4, б, в).

Сила упругости изменяется в процессе деформации пружины. Для нахождения работы силы упругости можно взять среднее значение модуля силы (т.к. сила упругости линейно зависит от x ) и умножить на модуль перемещения:

\(~A = F_{upr-cp} \cdot (x_1 - x_2)\) , (13)

где \(~F_{upr-cp} = k \cdot \frac{x_1 - x_2}{2}\) . Отсюда

\(~A = k \cdot \frac{x_1 - x_2}{2} \cdot (x_1 - x_2) = k \cdot \frac{x^2_1 - x^2_2}{2}\) или \(~A = -\left(\frac{k \cdot x^2_2}{2} - \frac{k \cdot x^2_1}{2} \right)\) . (14)

Физическая величина, равная половине произведения жесткости тела на квадрат его деформации, называется потенциальной энергией упруго деформированного тела:

\(~E_p = \frac{k \cdot x^2}{2}\) . (15)

Из формул (14) и (15) следует, что работа силы упругости равна изменению потенциальной энергии упруго деформированного тела, взятому с противоположным знаком:

\(~A = -(E_{p2} - E_{p1})\) . (16)

Если x 2 = 0 и x 1 = х , то, как видно из формул (14) и (15),

\(~E_p = A\) .

Физический смысл потенциальной энергии деформированного тела

потенциальная энергия упруго деформированного тела равна работе, которую совершает сила упругости при переходе тела в состояние, в котором деформация равна нулю.

Потенциальная энергия характеризует взаимодействующие тела, а кинетическая энергия – движущиеся тела. И потенциальная, и кинетическая энергия изменяются только в результате такого взаимодействия тел, при котором действующие на тела силы совершают работу, отличную от нуля. Рассмотрим вопрос об изменениях энергии при взаимодействиях тел, образующих замкнутую систему.

Замкнутая система – это система, на которую не действуют внешние силы или действие этих сил скомпенсировано . Если несколько тел взаимодействуют между собой только силами тяготения и силами упругости и никакие внешние силы на них не действуют, то при любых взаимодействиях тел работа сил упругости или сил тяготения равна изменению потенциальной энергии тел, взятому с противоположным знаком:

\(~A = -(E_{p2} - E_{p1})\) . (17)

По теореме о кинетической энергии, работа тех же сил равна изменению кинетической энергии:

\(~A = E_{k2} - E_{k1}\) . (18)

Из сравнения равенств (17) и (18) видно, что изменение кинетической энергии тел в замкнутой системе равно по абсолютному значению изменению потенциальной энергии системы тел и противоположно ему по знаку:

\(~E_{k2} - E_{k1} = -(E_{p2} - E_{p1})\) или \(~E_{k1} + E_{p1} = E_{k2} + E_{p2}\) . (19)

Закон сохранения энергии в механических процессах :

сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой силами тяготения и си-лами упругости, остается постоянной.

Сумма кинетической и потенциальной энергии тел называется полной механической энергией .

Приведем простейший опыт. Подбросим вверх стальной шарик. Сообщив начальную скорость υ нач, мы придадим ему кинетическую энергию, из-за чего он начнет подниматься вверх. Действие силы тяжести приводит к уменьшению скорости шарика, а значит, и его кинетической энергии. Но шарик поднимается выше и выше и приобретает все больше и больше потенциальной энергии (Е p = m∙g∙h ). Таким образом, кинетическая энергия не исчезает бесследно, а происходит ее превращение в потенциальную энергию.

В момент достижения верхней точки траектории (υ = 0) шарик полностью лишается кинетической энергии (Е k = 0), но при этом его потенциальная энергия становится максимальной. Дальше шарик меняет направление движения и с увеличивающейся скоростью движется вниз. Теперь происходит обратное превращение потенциальной энергии в кинетическую.

Закон сохранения энергии раскрывает физический смысл понятия работы :

работа сил тяготения и сил упругости, с одной стороны, равна увеличению кинетической энергии, а с другой стороны, – уменьшению потенциальной энергии тел. Следовательно, работа равна энергии, превратившейся из одного вида в другой.

Закон об изменении механической энергии

Если система взаимодействующих тел не замкнута, то ее механическая энергия не сохраняется. Изменение механической энергии такой системы равно работе внешних сил:

\(~A_{vn} = \Delta E = E - E_0\) . (20)

где Е и Е 0 – полные механические энергии системы в конечном и начальном состояниях соответственно.

Примером такой системы может служить система, в которой наряду с потенциальными силами действуют непотенциальные силы. К непотенциальным силам относятся силы трения. В большинстве случаев, когда угол между силой трения F r тела составляет π радиан, работа силы трения отрицательна и равна

\(~A_{tr} = -F_{tr} \cdot s_{12}\) ,

где s 12 – путь тела между точками 1 и 2.

Силы трения при движении системы уменьшают ее кинетическую энергию. В результате этого механическая энергия замкнутой неконсервативной системы всегда уменьшается, переходя в энергию немеханических форм движения.

Например, автомобиль, двигавшийся по горизонтальному участку дороги, после выключения двигателя проходит некоторый путь и под действием сил трения останавливается. Кинетическая энергия поступательного движения автомобиля стала равной нулю, а потенциальная энергия не увеличилась. Во время торможения автомобиля произошло нагревание тормозных колодок, шин автомобиля и асфальта. Следовательно, в результате действия сил трения кинетическая энергия автомобиля не исчезла, а превратилась во внутреннюю энергию теплового движения молекул.

Закон сохранения и превращения энергии

при любых физических взаимодействиях энергия превращается из одной формы в другую.

Иногда угол между силой трения F tr и элементарным перемещением Δr равен нулю и работа силы трения положительна:

\(~A_{tr} = F_{tr} \cdot s_{12}\) ,

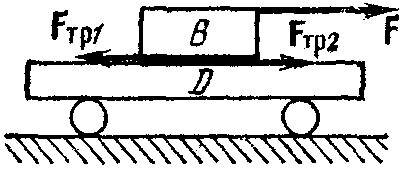
Пример 1 . Пусть, внешняя сила F действует на брусок В , который может скользить по тележке D (рис. 5). Если тележка перемещается вправо, то работа силы трения скольжения F tr2 , действующей на тележку со стороны бруска, положительна:

Пример 2 . При качении колеса его сила трения качения направлена вдоль движения, так как точка соприкосновения колеса с горизонтальной поверхностью двигается в направлении, противоположном направлению движения колеса, и работа силы трения положительна (рис. 6):

Литература

Кабардин О.Ф. Физика: Справ. материалы: Учеб. пособие для учащихся. – М.: Просвещение, 1991. – 367 с.
Кикоин И.К., Кикоин А.К. Физика: Учеб. для 9 кл. сред. шк. – М.: Про-свещение, 1992. – 191 с.
Элементарный учебник физики: Учеб. пособие. В 3 т. / Под ред. Г.С. Ландсберга: т. 1. Механика. Теплота. Молекулярная физика. – М.: Физматлит, 2004. – 608 с.
Яворский Б.М., Селезнев Ю.А. Справочное руководство по физике для поступающих в вузы и самообразования. – М.: Наука, 1983. – 383 с.

Начнем с определения. Работа А силы F при перемещении х тела, к которому она приложена, определяется как скалярное произведение векторов F и х .

А= F ·х= Fxcosα . (2.9.1)

Где α – угол между направлениями силы и перемещения.

Сейчас нам пригодится выражение (1.6 а), которое получено при равноускоренном движении. Но вывод мы сделаем универсальный, который и называется теоремой о кинетической энергии. Итак, перепишем равенство (1.6 а)

a · x =(V 2 –V 0 2)/2.

Умножим обе части равенства на массу частицы, получим

Fx =m(V 2 –V 0 2)/2.

Окончательно

А= m V 2 /2 – m V 0 2 /2. (2.9.1)

Величину Е = m V 2 /2 называют кинетической энергией частицы.

Вы привыкли, что в геометрии теоремы имеют свою устную формулировку. Чтобы не отстать от этой традиции, представим теорему о кинетической энергии в виде текста.

Изменение кинетической энергии тела равно работе всех сил, действующих на него.

Данная теорема носит универсальный характер, т. е. справедлива для любого вида движения. Однако точное её доказательство связано с применением интегрального исчисления. Поэтому мы его опускаем.

Рассмотрим пример движения тела в поле тяжести. Работа силы тяжести не зависит от вида траектории, соединяющей начальную и конечную точки, а определяется только разностью высот в начальном и конечном положениях:

А=mg(h 1 –h 2). (2.9.2)

Примем какую-нибудь точку поля тяжести за начало отсчета и будем рассматривать работу, совершаемую силой тяжести при перемещении частицы в эту точку из другой произвольной точки Р , находящейся на высоте h . Эта работа равна mgh и называется потенциальной энергией Е п частицы в точке Р :

Е п = mgh (2.9.3)

Теперь преобразуем равенство (2.9.1), механическая теорема о кинетической энергии примет вид

А= m V 2 /2 – m V 0 2 /2= Е п1 – Е п2 . (2.9.4)

m V 2 /2+ Е п2 = m V 0 2 /2+ Е п1 .

В этом равенстве в левой части стоит сумма кинетической и потенциальной энергии в конечной точке траектории, а в правой – в начальной.

Эту сумму называют полной механической энергией. Будем обозначать ее Е .

Е = Е к + Е п.

Мы пришли к закону сохранения полной энергии: в замкнутой системе полная энергия сохраняется.

Однако следует сделать одно замечание. Пока мы рассматривали пример так называемых консервативных сил . Эти силы зависят только от положения в пространстве. А работа, совершаемая такими силами при перемещении тела из одного положения в другое, зависит только от этих двух положений и не зависит от пути. Работа, совершаемая консервативной силой, является механически обратимой, т. е. меняет свой знак при возврате тела в исходное положение. Сила тяжести является консервативной силой. В дальнейшем мы познакомимся с другими видами консервативных сил, например, с силой электростатического взаимодействия.

Но в природе бывают и неконсервативные силы . Например, сила трения скольжения. Чем больше путь частицы, тем большую работу совершает сила трения скольжения, действующая на эту частицу. Кроме того, работа силы трения скольжения всегда отрицательна, т. е. «вернуть» энергию такая сила не может.

Для замкнутых систем полная энергия, конечно, сохраняется. Но для большинства задач механики более важным является частный случай закона сохранения энергии, а именно закон сохранения полной механической энергии. Вот его формулировка.

Если на тело действуют только консервативные силы, то его полная механическая энергия, определяемая как сумма кинетической и потенциальной энергий, сохраняется .

В дальнейшем нам понадобятся ещё два важных равенства. Как всегда, вывод заменим простой демонстрацией частного случая поля тяжести. Но вид этих равенств будет справедлив для любых консервативных сил.

Приведем равенство (2.9.4) к виду

А= F ∆x = Е п1 – Е п2 = –( Е п.кон – Е п.нач)= – ∆U.

Здесь мы рассмотрели работу А при перемещении тела на расстояние ∆x . Величину ∆U, равную разности конечной и начальной потенциальной энергии, называют изменением потенциальной энергии. А полученное равенство заслуживает отдельной строчки и специального номера. Поспешим его присвоить ему:

А= – ∆U (2.9.5)

Отсюда же вытекает математическая связь между силой и потенциальной энергией:

F = – ∆U/∆x (2.9.6)

В общем случае, не связанном с полем тяжести, равенство (2.9.6) представляет собой простейшее дифференциальное уравнение

F = – dU / dx .

Последний пример рассмотрим без доказательства. Гравитационная сила описывается законом всемирного тяготения F (r )= GmM / r 2 и является консервативной. Выражение для потенциальной энергии гравитационного поля имеет вид:

U (r )= – GmM / r .

Автор : – Разберем простой случай. На тело массой m, находящееся на горизонтальной плоскости, действует в течение промежутка времени Т горизонтальная сила F . Трение отсутствует. Чему равна работа силы F ?

Студент : – За время Т тело переместится на расстояние S=а Т 2 /2, где а =F /m. Следовательно, искомая работа есть А =F S=F 2 T 2 /(2m).

Автор : Все правильно, если считать, что тело покоилось до того, как на него начала действовать сила. Несколько усложним задачу. Пусть до начала действия силы тело двигалось прямолинейно и равномерно с некоторой скоростью V 0 , сонаправленной с внешней силой. Чему теперь равна работа за время Т ?

Студент : – Для расчета перемещения возьму более общую формулу S= V 0 T + а Т 2 /2, для работы получаю А =F (V 0 T + а Т 2 /2). Сравнивая с предыдущим результатом, вижу, что одна и та же сила за одинаковые промежутки времени производит разную работу.

Тело массой m скользит вниз по наклонной плоскости с углом наклона α. Коэффициент трения скольжения тела о плоскость k . На тело все время действует горизонтальная сила F . Чему равна работа этой силы при перемещении тела на расстояние S?

Студент : – Произведем расстановку сил и найдем их равнодействующую. На тело действует внешняя сила F, а также силы тяжести, реакции опоры и трения.

Студент : – Получается, что работа А= F Scos α и всё. Меня действительно подвела привычка каждый раз искать все силы, тем более что в задаче указана масса и коэффициент трения.

Студент : – Работу силы F я уже вычислил: А 1 = F S cos α. Работа силы тяжести есть А 2 =mgSsin α. Работа силы трения … отрицательна, т. к. векторы силы и перемещения противоположно направлены: А 3 = – kmgScos α. Работа силы реакции N равна нулю, т. к. сила и перемещение перпендикулярны. Правда, я не очень понимаю смысла отрицательной работы?

Автор : – Это означает, что работа данной силы уменьшает кинетическую энергию тела. Кстати. Давайте обсудим движение тела, изображенного на рис.2.9.1, с точки зрения закона сохранения энергии. Для начала найдите суммарную работу всех сил.

Студент : – А = А 1 + А 2 + А 3 = FScos α+ mgSsin α– kmgScos α.

По теореме о кинетической энергии разность кинетических энергий в конечном и начальном состояниях равна совершенной над телом работе:

Е к –Е н =А .

Студент : – Может быть, это были другие уравнения, не относящиеся к данной задаче?

Автор : – Но все уравнения должны давать одинаковый результат. Дело в том, что потенциальная энергия содержится в скрытом виде в выражении для полной работы. Действительно, вспомните А 2 =mgSsin α=mgh, где h – высота спуска тела. Получите, теперь из теоремы о кинетической энергии выражение закона сохранения энергии.

Студент : – Так как mgh=U н – U к, где U н и U к соответственно начальная и конечная потенциальные энергии тела, то имеем:

mV н 2 /2 + U н + А 1 + А 3 = mV к 2 /2+ U к.

Студент : – Это, по-моему, легко. Работа силы трения по модулю как раз и равна количеству теплоты Q . Поэтому Q = kmgScos α.

Студент : mV н 2 /2 + U н + А 1 – Q = mV к 2 /2+ U к.

Автор : – Теперь несколько обобщим определение работы. Дело в том, что соотношение (2.9.1) верно только для случая действия постоянной силы. Хотя есть немало случаев, когда сила сама зависит от перемещения частицы. Приведите пример.

Студент : – Первое, что приходит в голову, это растяжение пружины. По мере перемещения незакрепленного конца пружины сила, все увеличивается. Второй пример связан с маятником, который, как мы знаем, сложнее удержать при больших отклонениях от положения равновесия.

Автор : – Хорошо. Давайте остановимся на примере с пружиной. Сила упругости идеальной пружины описывается законом Гука, в соответствии с которым при сжатии (или растяжении) пружины на величину х возникает сила, противоположно направленная смещению, линейно зависящая от х . Запишем закон Гука в виде равенства:

F = – kx (2.9.2)

Здесь k – коэффициент жесткости пружины, x – величина деформации пружины. Изобразите график зависимости F (x ).

Студент : Мой чертеж представлен на рисунке.

Рис.2.9.2

Левая половина графика соответствует сжатию пружины, а правая – растяжению.

Автор : – Теперь вычислим работу силы F при перемещении от х =0 до х = S. Для этого существует общее правило. Если нам известна общая зависимость силы от смещения, то работа на участке от х 1 до х 2 есть площадь под кривой F (x ) на этом отрезке.

Студент : – Значит, работа силы упругости при перемещении тела от х =0 до х =S отрицательна, а модуль её равен площади прямоугольного треугольника: А = kS 2 /2.

А = kх 2 /2. (2.9.3)

Эта работа превращается в потенциальную энергию деформированной пружины.

История.

Резерфорд демонстрировал слушателям распад радия. Экран то светился, то темнел.

– Теперь вы видите, – сказал Резерфорд, – что ничего не видно. А почему ничего не видно, вы сейчас увидите.

Вопросы и задания

1. Перечислите ситуации, встречающиеся в повседневной жизни, в которых участвуют неконсервативные силы.

2. Вы медленно поднимаете книгу со стола на высокую полку. Перечислите силы, действующие на книгу, и определите, какие из них являются консервативными, а какие нет.

3. Результирующая сила, действующая на частицу, консервативна и увеличивает её кинетическую энергию на 300 Дж . Каково при этом изменение а) потенциальной энергии частицы, б) её полной энергии?

4. Имеет ли физический смысл следующее утверждение: использование шестов из гибкого пластика в прыжках в высоту привело к росту результатов благодаря тому, что большая его гибкость дает дополнительную упругую энергию, преобразуемую в потенциальную энергию поля тяжести?

5. Имеется наклонная плоскость, один конец которой поднят на высоту Н . Тело массой М скатывается (без начальной скорости) из верхней точки. Зависит ли скорость этого тела у основания наклонной плоскости от угла, который она составляет с горизонтом, если а) трение отсутствует, б) трение имеется?

6. Почему мы все же утомляемся, когда сначала взбираемся на гору, а потом спускаемся с нее? Ведь полная работа в поле тяжести равна нулю.

7. Этот пример ещё жестче. Представьте, что Вы держите гантелю на вытянутой руке. Не бойтесь, она не очень тяжелая. Но все же рука устает. А механической работы никакой нет, т. к. нет движения. Куда расходуется энергия Ваших мышц?

8. Пружина массой m покоится в вертикальном положении на столе. Сможет ли пружина, подпрыгнув, оторваться от стола, после того как Вы сожмете её, надавив сверху, а затем отпустите? Объясните свой ответ, используя закон сохранения энергии.

9. Что происходит с потенциальной энергией, которую имела вода в верхней части водопада, когда вода достигнет его основания? А что случится с кинетической и полной энергией?

10. Опытные туристы предпочитают перешагивать через упавшее бревно, а не, наступив на него, спрыгивать с противоположной стороны. Объясните явление.

11. Два человека находятся на разных платформах, которые движутся относительно друг друга со скоростью V. Они наблюдают за бревном, которое тянут по шероховатой горизонтальной поверхности. Совпадают ли полученные этими людьми значения: а) кинетической энергии бревна; б) полной работы, совершаемой над телом; в) механической энергии, перешедшей в тепловую из-за наличия трения? Не противоречит ли ответ на вопрос в) ответам на вопросы а) и б)?

12. Откуда берется кинетическая энергия автомобиля при равномерном его ускорении из состояния покоя? Как связать возрастание кинетической энергии с наличием силы трения между шинами и шоссе?

13. Зимой Земля приближается к Солнцу на кратчайшее расстояние. Когда потенциальная энергия Земли наибольшая?

14 Может ли полная механическая энергия быть отрицательной? Приведите примеры.

15. В какой точке величина сила наибольшая? Для каждой из обозначенных цифрами точек укажите, в каком направлении действует сила. Какая точка соответствует положению равновесия?

Задачи

16. Пуля пробивает закрепленную доску при минимальной скорости 200 м/с . С какой скоростью должна лететь пуля для того, чтобы пробить эту доску, подвешенную на длинной нити? Масса пули 15г , масса доски 90г , пуля попадает точно в центр доски перпендикулярно её поверхности.

17. Деревянный шар массой М =1 кг висит на шнуре так, что расстояние от точки подвеса шнура до центра шара равно L = 1 м . В шар попадает горизонтально летящая со скоростью V 1 =400 м/с пуля массой m = 10 г , которая пробивает шар точно по диаметру и вылетает из него со скоростью V 2 =230 м/с . Определите угол  максимального отклонения подвеса от вертикали. Сопротивлением воздуха и временем пробивания шара пулей пренебречь.

18. На плоскости, наклоненной к горизонту под углом α, лежат два тела массой m . Коэффициент трения между телами и плоскостью k >tg α. Телам придают одинаковые встречные скорости V . При каком максимальном начальном расстоянии L между телами они столкнутся?

19. Тележка скатывается по гладким рельсам, образующим вертикальную петлю радиуса R . С какой минимальной высоты H min должна скатиться тележка для того, чтобы она не покинула рельсов по всей их длине? Каково будет движение тележки, если она скатывается с высоты h , меньшей H min ?

20. Определите силу, действующую на вертикальную стенку со стороны падающей гантели, в тот момент, когда ось гантели составляет угол  с горизонтом. Гантель начинает свое движение из вертикального положения без начальной скорости. Масса каждого шарика гантели m.

21. На нити длиной 2h подвешен грузик массой m . На расстоянии h под точкой подвеса вбит гвоздь. Нить отклонили из положения равновесия на угол /2 и отпустили. На какую максимальную высоту поднимется грузик после прохождения положения равновесия?

22. Подставка массой M с полусферической выемкой радиуса R стоит на гладкой горизонтальной плоскости. Малое тело массой m кладут на край выемки и отпускают. Найти скорости тела и подставки, силу, действующую на тело в момент прохождения нижней точки

23. Груз массой m , подвешенный на пружине жесткости k , удерживается подставкой так, что пружина находится в недеформированном состоянии. Подставку внезапно убирают. Найти максимальное удлинение пружины и максимальную скорость груза.

24. От груза, подвешенного на пружине жесткости k , отрывается часть массой m . На какую высоту поднимется после этого оставшаяся часть груза?

25. C какой силой надо надавить на верхний груз массой m , чтобы нижний груз массой M , соединенный с верхним пружиной жесткости k , оторвался от пола после прекращения действия силы?

26. На горизонтальной плоскости лежат два тела массами m 1 и m 2 , соединённых недеформированной пружиной. Найти, какую наименьшую постоянную силу нужно приложить к левому телу, чтобы сдвинулось правое. Коэффициент трения тел о плоскость .

Теорема о кинетической энергии формулируется так. Сумма работы всех сил (консервативных и неконсервативных), приложенных к телу, равна приращению его кинетической энергии. С помощью этой теоремы можно обобщить закон сохранения механической энергии на случай незамкнутой (неизолированной) системы : приращению полной механической энергии системы равно работе сторонних сил над системой.

Траектория

Траекторией называется воображаемая линия, описываемая телом при движении. В зависимости от формы траектории движения бывают криволинейные и прямолинейные. Примеры криволинейного движения: движение тела, брошенного под углом к горизонту (траектория – парабола), движение материальной точки по окружности.

Трение

Возникает между двумя телами в плоскости соприкосновения их поверхностей и сопровождается диссипацией (рассеиванием) энергии. Механическая энергия системы, в которой есть трение, может только уменьшаться. Наука, изучающая трение, называется трибологией. Опытным путем установлено, что максимальная сила трения покоя и сила трения скольжения не зависит от площади соприкосновения тел и пропорциональна силе нормального давления, прижимающей поверхности друг к другу. Коэффициент пропорциональности при этом называется коэффициентом трения (покоя или скольжения).

Третий закон Ньютона

Третий закон Ньютона - физический закон, в соответствии с которым силы взаимодействия двух материальных точек равны по модулю, противоположны по направлению и действуют вдоль прямой, соединяющей эти точки. Как и прочие законы Ньютона, третий закон справедлив только для инерциальных систем отсчета . Краткая формулировка третьего закона: действие равно противодействию.

Третья космическая скорость

Третья космическая скорость - минимальная скорость , необходимая для того, чтобы космический аппарат, запущенный с Земли, преодолел притяжение Солнца и покинул Солнечную систему. Если бы Земля в момент запуска была неподвижна и не притягивала тело к себе, то третья космическая скорость была бы равна 42 км/с. С учетом скорости орбитального движения Земли (30 км/с) третья космическая скорость равна 42-30 = 12 км/с (при запуске в направлении орбитального движения) или 42+30 = 72 км/с (при запуске в противоположном направлении). Если учесть еще и силу притяжения к Земле, то для третьей космической скорости получим значения от 17 до 73 км/с.

Ускорение

Ускорение - векторная величина, характеризующая быстроту изменения скорости . При произвольном движении ускорение определяется как отношение приращения скорости к соответствующему промежутку времени. Если устремить этот промежуток времени к нулю, получим мгновенное ускорение. Значит, ускорение есть производная от скорости по времени. Если рассматривается конечный промежуток времени Δt, то ускорение называется средним. При криволинейном движении полное ускорение складывается из тангенциального (касательного) и нормального ускорения .

Угловая скорость

Угловая скорость - векторная величина, характеризующая вращательное движение твердого тела и направленная по оси вращения согласно правилу правого винта. Средняя угловая скорость численно равна отношению угла поворота к соответствующему промежутку времени. Взяв производную от угла поворота по времени, получим мгновенную угловую скорость. Единицей угловой скорости в СИ является рад/с.

Ускорение свободного падения

Ускорение свободно падающего тела - ускорение, с которым движется тело под действием силы тяготения. Ускорение свободного падения одинаково для всех тел, независимо от их массы . На Земле ускорение свободно падающего тела зависит от высоты над уровнем моря и от географической широты и направления к центру Земли. На широте 45 0 и на уровне моря ускорение свободно падающего тела g = 9.80665 м/с 2 . В учебных задачах обычно полагают g = 9,81 м/с 2 .

Физический закон

Физический закон - необходимая, существенная и устойчиво повторяющаяся связь между явлениями, процессами и состояниями тел. Познание физических законов составляет основную задачу физической науки.

50. Физический маятник

Физический маятник - абсолютно твердое тело , имеющее ось вращения. В поле тяготения физический маятник может совершать колебания около положения равновесия, при этом массу системы нельзя считать сосредоточенной в одной точке. Период колебаний физического маятника зависит от момента инерции тела и от расстояния от оси вращения до центра масс .

Энергия (от греч. energeia – деятельность)

Энергия - скалярная физическая величина, являющаяся общей мерой различных форм движения материи и мерой перехода движения материи из одних форм в другие. Основные виды энергии: механическая, внутренняя, электромагнитная, химическая, гравитационная, ядерная. Одни виды энергии могут превращаться в другие в строго определенных количествах (см. также Закон сохранения и превращения энергии ).

Термодинамика и молекулярная физика

Под элементарной работой dА, совершаемой силой на элементарном перемещении , называют величину, равную скалярному произведению на

где угол a - угол между векторами силы и перемещением (рис.1.22,а);

Модуль вектора элементарного перемещения или элементарный путь пройденной точкой приложения силы.

Работа силы на конечном перемещении равна сумме элементарных работ:

. (1.61)

Если сила постоянна ( =const), то ее работа на прямолинейном участке длины l запишется следующим образом:

. (1.62)

Работа силы может быть положительной, отрицательной или равной нулю. Так, работы постоянных сил, приложенных к телу (рис.1.22б) на горизонтальном участке пути l, равны:

Чтобы ввести понятие о кинетической энергии W k тела, запишем элементарную работу dA силы в другом виде (см. 1.2.2):

Тогда для работы силы , переводящей тело из состояния 1 (скорость тела ) в состояние 2 (скорость тела ) можно записать:

Из полученной формулы следует, что работа силы равна разности двух величин, определяющих начальное (скорость ) и конечное (скорость ) состояния тела. При этом условия перехода из состояния 1 в состояние 2 не оказывают влияние на записанное выражение. Поэтому можно ввести функцию состояния тела, его кинетическую энергию W к как СФВ, характеризующую способность тела совершать работу за счет изменения скорости его движения и равную

В этом выражении постоянную величину выбирают, предположив, что при нулевой скорости движения тела его кинетическая энергия равна нулю, поэтому

Кинетическая энергия тел не зависит от того, как была достигнута данная скорость u, она является функцией состояния тела, положительной величиной, зависящей от выбора системы отсчета.

Введение W к позволяет сформулировать теорему о кинетической энергии, согласно которой алгебраическая сумма работ всех сил, действующих на тело, равна приращению кинетической энергии тела:

Эта теорема широко используется для анализа взаимодействия тел не только в механике, но и в других разделах курса физики, таких как электростатика, постоянный ток, электромагнетизм, колебания и волны и т.д.

1.4.2. Кинетическая энергия вращающегося а.т.т.

Возьмем а.т.т., вращающееся вокруг неподвижной оси с угловой скоростью (рис.1.16,б). Представим тело в виде совокупности м.т. массы dm , тогда для кинетической энергии тела можно записать:

Итак, кинетическая энергия а.т.т. вращающегося относительно неподвижной оси вращения, определяется по формуле

Если тело одновременно участвует в поступательном (плоском) и вращательном движениях (например, движение цилиндра без скольжения по плоскости, рис.1.23,а), то его кинетическую энергию можно получить

Рис.1.23

как сумму кинетической энергии поступательного движения тела вместе с осью вращения, проходящей через его центр масс (точка О ), со скоростью и вращательного движения тела относительно этой оси с угловой скоростью

. (1.67)

Для сплошного (I 1 =1/2mR 2 ) и тонкостенного (I 2 =mR 2 ) цилиндров одинаковой массы m и радиуса R кинетические энергии запишутся таким образом:

Полученные формулы для кинетической энергии цилиндров позволяют объяснить опыт по различию времени их скатывания с наклонной плоскости высотой h и длиной l (рис.1.23,б). Так, согласно закону сохранения энергии (силой трения при движении цилиндров практически можно пренебречь) получим

где обозначают скорости сплошного и полого цилиндров у основания наклонной плоскости.

При скатывании цилиндров центр их масс движется равноускоренно без начальной скорости и поэтому согласно формуле (1.13) можно записать:

т.е. на скатывание полого цилиндра требуется большее время, чем для сплошного цилиндра.

Качественно это можно объяснить тем, что полый цилиндр является более инертным, чем сплошной (для него момент инерции относительно оси вращения больше), и поэтому он медленнее изменяет свою скорость и поэтому тратит больше времени на скатывание с наклонной плоскости.

Как видно из рис.1.23,а, модули скоростей точек на поверхности цилиндра будут разными (u В =0, , u А =2u) в связи с тем, что эти точки участвуют одновременно и в поступательном и в вращательном движениях со скоростями и , причем для каждой точки направлена по касательной к поверхности цилиндра и равна по модулю u ( ).

Отметим, что движение цилиндра можно рассматривать и как ряд последовательных вращений вокруг мгновенной оси, проходящей через точку С (рис.1.23,а) с угловой скоростью w. Причем и в этом случае кинетическая энергия тела также определяется формулой (1.67).

работа равнодействующей сил, приложенных к телу, равна изменению кинетической энергии тела.

A =Ek 2−Ek 1=m ⋅υ 22−0=m ⋅υ 22 .

42) Потенциальные поля

Потенциальное поле

консервативное поле, векторное поле, циркуляция которого вдоль любой замкнутой траектории равна нулю. Если П. п. - силовое поле, то это означает равенство нулю работы сил поля вдоль замкнутой траектории. Для П. п. а (М ) существует такая однозначная функция u (М )(Потенциал поля), что а = gradu (см. Градиент). Если П. п. задано в односвязной области Ω, то потенциал этого поля может быть найден по формуле

в которой AM - любая гладкая кривая, соединяющая фиксированную точку А из Ω с точкой М, t - единичный вектор касательной кривой AM и / - длина дуги AM, отсчитываемая от точки А. Если а (М ) - П. п., то rot a = 0 (см. Вихрь векторного поля). Обратно, если rot а = 0 и поле задано в односвязной области и дифференцируемо, то а (М ) - П. п. Потенциальными являются, например, электростатическое поле, поле тяготения, поле скоростей при безвихревом движении.

43) Потенциальная энергия

Потенциальная энергия - скалярная физическая величина, характеризующая способность некого тела (или материальной точки) совершать работу за счет его нахождения в поле действия сил. Другое определение: потенциальная энергия - это функция координат, являющаяся слагаемым в лагранжианесистемы, и описывающая взаимодействие элементов системы. Термин «потенциальная энергия» был введен в XIX веке шотландским инженером и физиком Уильямом Ренкином.

Единицей измерения энергии в СИ является Джоуль.

Потенциальная энергия принимается равной нулю для некоторой конфигурации тел в пространстве, выбор которой определяется удобством дальнейших вычислений. Процесс выбора данной конфигурации называетсянормировкой потенциальной энергии .

Корректное определение потенциальной энергии может быть дано только в поле сил, работа которых зависит только от начального и конечного положения тела, но не от траектории его перемещения. Такие силы называются консервативными.

Также потенциальная энергия является характеристикой взаимодействия нескольких тел или тела и поля.

Любая физическая система стремится к состоянию с наименьшей потенциальной энергией.

Потенциальная энергия упругой деформации характеризует взаимодействие между собой частей тела.

Потенциальная энергия в поле тяготения Земли вблизи поверхности приближённо выражается формулой:

где E p - потенциальная энергия тела, m - масса тела, g - ускорение свободного падения, h - высота положения центра масс тела над произвольно выбранным нулевым уровнем.

44) Связь силы и потенциальной энергии

Каждой точке потенциального поля соответствует, с одной стороны, некоторое значение вектора силы , действующей на тело, и, с другой стороны, некоторое значение потенциальной энергии . Следовательно, между силой и потенциальной энергией должна существовать определенная связь.

Для установления этой связи вычислим элементарную работу , совершаемую силами поля при малом перемещении тела, происходящем вдоль произвольно выбранного направления в пространстве, которое обозначим буквой . Эта работа равна

где - проекция силы на направление .

Поскольку в данном случае работа совершается за счет запаса потенциальной энергии , она равна убыли потенциальной энергии на отрезке оси :

Из двух последних выражений получаем

Последнее выражение дает среднее значение на отрезке . Чтобы

получить значение в точке нужно произвести предельный переход:

в математике вектор ,

где а - скалярная функция х, у, z, называется градиентом этого скаляра обозначается символом . Следовательно сила равна градиенту потенциальной энергии, взятого с обратным знаком

45) Закон сохранения механической энергии